倍数・公倍数
倍数
教科書の説明をそのまま書きます。
「ある整数の整数倍になっている整数をその整数の倍数といいます。」
なななにを言いたいか ぜんぜんわからない…
こんな説明 どうでしょうか。
①掛け算九九の答え
②○で割り切れる数のことを○の倍数といいます。
簡単な数字をあてはめます。
①3に1をかけて3
3に2をかけて6
3に3をかけて9
太字が3の倍数です。かけ算九九の3の段の答えになってます。そして3で割り切れる数のことを3の倍数といいます。
3で割り切れる数を「3の倍数」といいます。
【例 今年の「2022」なんてのも3の倍数です。3で割ると674で割り切れます。
公倍数 最小公倍数
2つ以上の数に共通する倍数のことです。そのなかで 一番小さい数を○と○の「最小公倍数」といいます。

じゃあ2と3の最大公倍数っていくつなの?

それはね 数は無限にあるから 未知数なんだって。
【問題5】
2と3の公倍数を小さい順に3つ答えましょう。

6と12と18です。
【問題6】
2と3の最小公倍数はいくつですか。
上の表で 2の倍数と3の倍数のかさなった いちばん小さい数は6です。
2と3の最小公倍数は 6 です。
はしご算で最小公倍数
【問題7】
18と27の最小公倍数を求めます。

※問題によっては、「公倍数を小さいほうから3つあげなさい」なんていうのがあります。公倍数は最小公倍数の倍数です。(例:54の2倍3倍……)
まず最小公倍数をもとめてから2倍3倍4倍します。
【問題8】
6と18と27の最小公倍数を求めます。
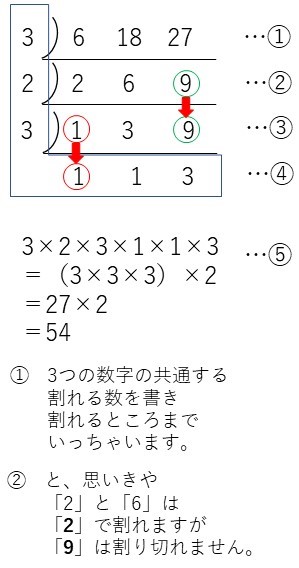

では上の問題の「18」を使って「そのままおろす」問題を説明します。
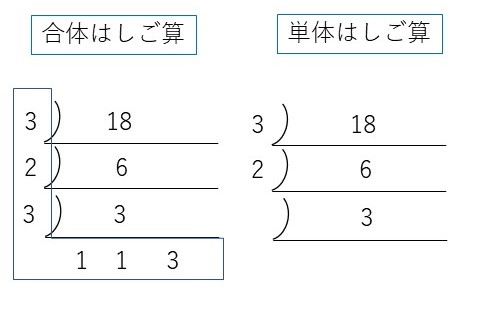
合体はしご算の 18の割り算の内容は 3×3×2×3
単体はしご算の 18の割り算の内容は 3×3×2 単体では×3が足りません。
続いて「27」も見てみます。
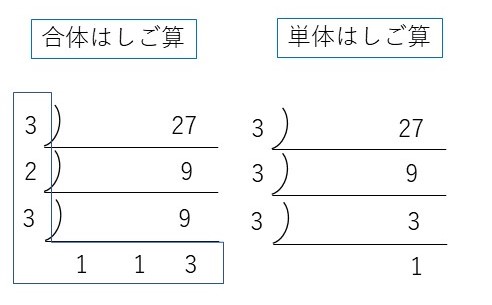
合体はしご算の 27の割り算の内容は 3×2×3×3
単体はしご算の 27の割り算の内容は 3×3×3 単体では×2が足りません。
ここで合体はしご算の「6」に注目します。
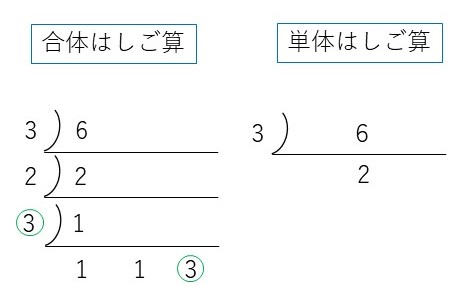
合体はしご算と 単体はしご算の違いは ×3 が ふたつともないことです。
18と27と6のそれぞれ足りなかった数は ×3と×2と×3と×3でした。全部かけると54。みんなで 共通の数をかけあって最小公倍数になっているんです。
この中で6は小さい数ですが、大きい数たちに合わせて 足並みをそろえた結果です。公倍数はみんなのかけ算の共通する倍数を探すことです。他の2つが 共通の約数を探している間に 自分は その共通の数をかけられているだけなので なんの心配もいりません。


さんちゃん あしなみ そろってないけど…

さんちゃん感激ぃぃ!
学校のワークテストはこんな感じの問題です。
【問題9】
公倍数を使う文章題は 文も長く 読み取る力が必要です。
あるバス停は 北駅行きのバスが8分ごと南駅行きのバスが9分ごとに 発車しています。午前8時30分に北駅行きと南駅行きのバスが同時に発車しました。
この次に 同時に発車するのは 午前何時何分ですか。

時計の計算ってむずかしいんだよぉ。
気絶しそうだよ。時計一周60分
ってぇのがいただけないんだよ。
60進法は すぐ身につくから 問題を整理しようね。
北駅行き 8分ごと
南駅行き 9分ごと
8時30分に出発
次に一緒に出発する時間をもとめます。


でた!72ってどう計算すればいいの⁈
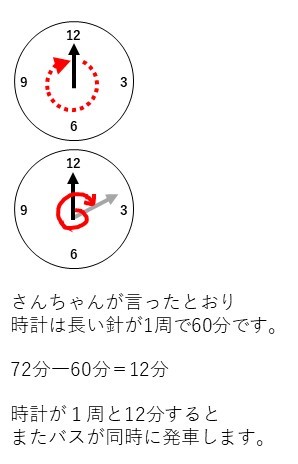

ここからは私たち タイムトラベラーよ。
さんちゃん よく想像してね。
さんちゃん 8時30分に駅に行くと バスが2台同時に出発したよ。バスは何色にする?

錆浅葱色と利休鼠色!。
ニンテンドースイッチで遊んで1時間経過したよ。
さんちゃん 時計を見て!
9時30分だ!あと12分だね。と、いうことは10分たすと9時40分。そこに2分たすから…

さんちゃん、バスが来たよ!錆浅葱色と利休鼠色だね。時計を見てくれる?

9時42分だ!
多少時間はかかりますが 時間経過を疑似体験しながらだと楽しみながら身につくようです。
【問題10】
次の2つの数の公約数を小さい順に3個かきましょう。
7と14
まずは はしご算をしてみましょう。
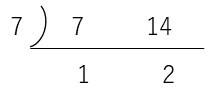
最小公倍数は 7×2=14 です。
14の倍数は
14の1倍の14
14の2倍の28
14の3倍の42
となります。
【問題11】
たて9cm横12cmの長方形のカードを 同じむきにならべて できるだけ小さい正方形をつくります。
正方形の一辺の長さは何㎝になりますか。
また その正方形には カードが何枚必要ですか。
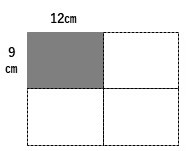

さんちゃん 問題がふたつあるね。

では やってみましょう。まず何枚かは考えず たてと横の長さの最小公倍数を求めます。縦と横両方の足並みがそろった数を探しだすことです。