小数どうしの割り算
これは現実社会での使用目的がちっとも浮かびません。ある世界では当たり前に使ってるのかもですが、主婦の私が使うとなると
0.5÷0.3 → 0.5個のケーキを0.3人でわる?
0.3人って 膝から下人間?

ありえない💦
小数はどうしても「1よりも小さい数」のイメージですが 2.5÷0.5 → 2.5mのリボンを0.5mずつわける。ならば実感がわきますよね。
ここで一番始めに書いた「割り算の意味」を思い出してください。
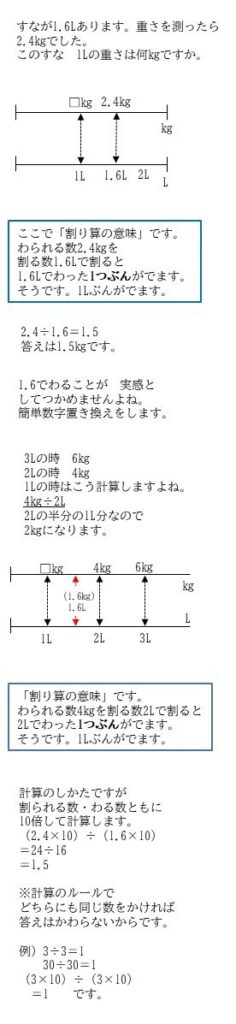
割り算は1つ分・1個分・1当たりなど 1を求めるための計算
わられる6を2で割ると 2で割った1つ分がでる。です。小数で割っても 1のときの答えを求めるので 答えはけっこう大きくなります。 0.3でわったりすると 答えは小さくなりそうなのにです。
【問題24】
その後は ひっ算の練習です。最後に忘れず 小数点をつけましょう。「みたて」が苦手な場合は
ゆっくりやりましょう。そしてどこが苦手か(九九など)を見つけ そのポイントまで戻りましょう。
【問題25】
5.85÷2.25を計算しましょう。

わり算には 割り切れない時もあります。「小数第1位」やら「1/10までの概数」やら聞きなれない言葉で問題を出してきます。章の最後に載せておきます!
【問題26】
14.95÷5.2を 計算しましょう。

次は文章題です。
【問題27】
3.6mの長さで8.82㎏の鉄の棒があります。この鉄の棒1mの重さは 何㎏ですか。

学校のワークテストはこんな感じの問題です。
【問題28】
下の図は ペンキの量とぬれる面積の関係を表にしたものです。[あ] にあてはまる数を求めましょう。

教科書では お得意の小数のわり算のまとめになります。今回もまた文章が 難解で…
わる数と商の大きさの関係は次のようになります。
わる数>1のとき 商<わられる数
わる数=1のとき 商=わられる数
わる数<1のとき 商>わられる数
どうでしょう。またわかりにくいのは 私だけでしょうか。
わかりやすい数字をあてはめてみます。
わる数が1より大きいと わられる数より答えが小さい
例:6(わられる数)÷ 3(わる数)=2
わる数が1だと わられる数と答えが同じ
例:6÷ 1=6
わる数が1より小さいと わられる数より答えが大きい
例:2÷0.5=4
小数で割ると 答えは大きくなるんですね。
「1あたり」をもとめるのが割り算です。
0.5よりも 1のほうが大きいです。
ですので答えは大きくなります。
【私事問題 2】
友人に誘われ アメリカから上陸した大スーパーマーケットに行きました。年会費もかかるので 同伴者として行けることはうれしい限りです。
しかし 3人家族には なかなか手ごわい品々です。誘ってもらった手前 何か買わねば…そうだ! 人気の柔軟剤入りの洗剤にするか!
「1.5ガロン…」
ガロンって新種のウルトラ怪獣か?1.5ガロンを 肩にかつぎ持ち帰り 家の空ボトルに詰め替えました。
ボトルの容量は750㏄。さて 1.5ガロンは何回詰め替えられるでしょう。
1ガロンは約3.8ℓです。
1.5ガロンだと約5.7ℓになります。
詰め替えボトルは750㏄なので0.75ℓです。
5.7ℓ÷0.75=7.6
7.6回分になりました。半年間は 甘~い きつ~い花の香りに包まれた生活でした。

赤いキャップと青いキャップの意味もわからん…
【算数用語の説明】
●四捨五入
4は捨てて5から入れます。
●「未満」とは
「未使用」なんて意味ですので 入れません。
例)18歳未満と言ったら18歳はダメです。19歳のお誕生日まで待ちましょう。
●それに対して以上以下は反対です。
「未」では含まれないのでその逆 こんどは含まれます。
例)18歳以上と言ったら18歳も大丈夫です。午前0時の18歳のお誕生日まで待ちましょう。
同じように 18歳以下と言ったら19歳になる寸前まで 入ります。
未満・超過(未満の逆)の範囲はせまく 以上以下は範囲がゆるいんですね。
●小数〇位までの概数
概数は「およその数」です。言われた桁のもう一つ下を 四捨五入です。
例)15.68の時 小数第一位までの概数と言ったら 0.08を四捨五入して繰り上げ15.7になります。
●整数○の位までの概数
言われた桁のもう一つ下を 四捨五入です。
例)1568の時 百の位の概数と言ったら 1568の68の6を四捨五入して繰り上げ1600になります。
●上から○けたの概数
言われた桁のもう一つ下を 四捨五入です。
例)1568の時 上から3けたの概数と言ったら 1568の4桁目の8を四捨五入して繰り上げ1570になります。
問題のもう一つ下の桁を操作しましょう。

