約数・公約数
約数
約数の説明です。
教科書には「ある整数を 割り切ることのできる整数を その整数の約数といいます」

そんなにすぐに割り切れる関係なの?ぼくたちは…

ごまかさないで…
では こんな説明でどうでしょう。
掛け算九九の「パキッとわれる数(わる数)」
6 ÷ 3
(わられる数)÷ (わる数)
3は6の約数です。
2つ以上の数に共通する約数を公約数といいます。
そのなかでも 一番大きい数を○と○の「最大公約数」といいます。

ねぇ 最小公約数っていくつなの?

ぜんぶ「1」だよ。どんな数も1でわれるからね。
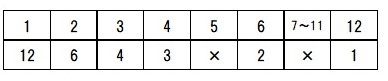
では 12の約数の見つけ方を 学校と同じようにやってみます。
①枠2段組みを適当につくります
②上下で掛け算をして 12になる組み合わせを左から 書き出します。
③表をつくると 見落としがちな 中盤の6✕2を書き漏らしに注意です。
つぎは公約数です。18と24の公約数をみつけます。
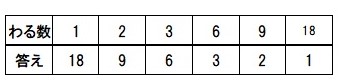
18の約数
24の約数
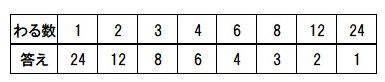
18と24を パキッとわりきる数で 共通する数は 1・2・3・6です。そのなかで一番大きい数が最大公約数です。6 です。
※最大公約数をさがす場合 小さい数のほうが約数が少ないので 小さい数から先に書き出し 次に大きい数の約数を探すと 時間の節約になります。
はしご算で公約数
では 公倍数と同じように「はしご算」のやり方です。
【問題12】
18と27の最大公約数を求めます。

※最大公約数の答えがでてから 公約数をもとめます。
公約数は最大公約数の約数です。(例:9の約数は 1・3・9です)
まず最大公約数をもとめてから その数の約数を求めます。
【問題13】
6と18と27の最大公約数を求めましょう。

【問題14】
64・144・176の最大公約数を求めましょう。

【問題15】
公約数を使う文章題は 公倍数同様難解です。
5年生が36人 6年生が48人います。ダンスをするため それぞれ同じ人数ずつに分かれて 5年生と6年生の混じったグループをつくります。余る人がでないように できるだけ多くのグループを つくります。 グループは いくつできますか。

あれあれ この問題 わり算じゃないの!
①まずはじめに 36人と48人の最大公約数をもとめます。2×2×3なので 12 となります。答えは 12です。はしご算で確認してみましょう。
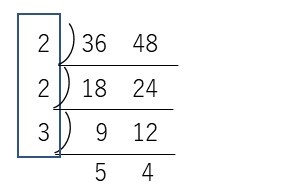
②できるだけ多くのグループをつくるのが目的です。そして「5.6年混合させなくては」なので 表をつくってみます。
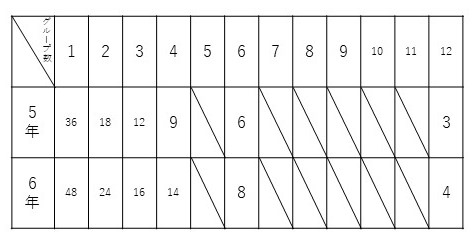
③グループが1つだと36人と48人
グループが2つだと18人と24人
グループが3つだと12人と16人……
④グループが12だと 5年生は3人6年生は4人の混合グループができます。

運動会の準備する先生 たいへんそうね。さんちゃんはどんなダンスをしたい?

学校のワークテストはこんな感じの問題です。
【問題16】
みかんが12個 いちごが16個あります。それぞれ同じ数ずつ どちらも余りがでないよう子供たちに分けます。できるだけ多くの子供にわけるとき 何人に わけられますか。
それでは 最大公約数を探しましょう。
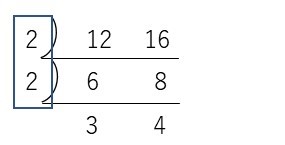
2×2=16 答えは4人です。
確認です。1人みかんは3個で4人だと3×4=12個。1人いちごは4個で4人だと4×4=12個。ぴったりでした。
【問題17】
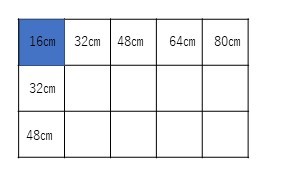
たて48㎝よこ80㎝の紙から同じ大きさの正方形を あまりがでないように切りたいとおもいます。できるだけ大きな正方形にわけるには 一辺を何㎝にすればよいですか。また この時正方形は 何枚できますか。
それでは 最大公約数を探しましょう。
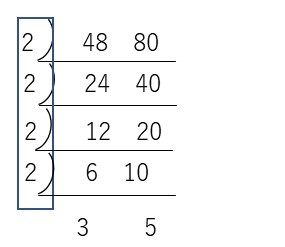
2×2×2×2=16
1辺が16㎝だとあまりがでないようです。
つぎに大きな紙で1辺16㎝の紙が何枚とれるか 計算してみましょう。
たて
48㎝を16㎝でわって何枚ならぶのかやってみます。
48÷16=3 たては3枚です。
よこ
80㎝を16㎝でわって何枚ならぶのかやってみます。
80÷16=5 よこは5枚です。
たて×よこ→ 3×5=15 15枚です。
16㎝の正方形が 15枚できます。